In Table 1 we characterize the lower end of the periodic distribution of atomic masses and identify the predicted Stellar Scale masses that should be observed as distinct, periodic peaks in stellar mass distributions. Stellar Scale discreteness and preferred mass peaks are discussed in several places at this website, such as Section 3.2 of Paper 1, Paper 6, and the August 2004 addition to the New Developments section.
Because the predicted Stellar Scale peaks are separated by only » 0.15 M8, because stellar mass estimates cannot be determined directly, and because the estimates are often based on numerous assumptions, at present we should have reasonable expectations for our ability to detect the hypothesized discreteness in Stellar Scale masses. A first step in examining the degree to which the Stellar Scale conforms to the predicted self-similar mass spectrum would be to see if there are observed stellar mass distributions that have peaks near the predicted masses listed in Table 1. That is the goal of this section of the website.
The stellar mass distributions shown below have been chosen specifically because they appear to conform to SSCP expectations. The second step in evaluating Stellar Scale discreteness will be to determine whether the results shown in this section are anomalous, or whether they are the first hints of true discreteness in stellar masses. At present, completing this second step seems like a distant prospect, but the accuracy of mass estimates is steadily improving, so there is hope.
Most of the samples shown below are new to this website, but let us start with several older ones that originally indicated that white dwarf stars might be a suitable class of stars for studying Stellar Scale discreteness. For each sample, solid red arrows indicate the positions of predicted peaks and a dotted arrow marks the location of the predicted N = 5 “gap”. For the relevant mass range of white dwarfs, roughly 0.35 M8 to 1.35 M8, we expect a small peak at 0.44 M8, a dominant peak at 0.58 M8, a “gap” (or under-representation) at 0.73 M8, a small peak at 0.87 M8 and much smaller peaks at 1.02 M8, 1.16 M8 and 1.31 M8.
Figures 1 through 5 exhibit relatively small samples of white dwarfs (WDs) and planetary nebula nuclei (PNN) that manifest some features of the predicted mass distribution.
FIGURE
1
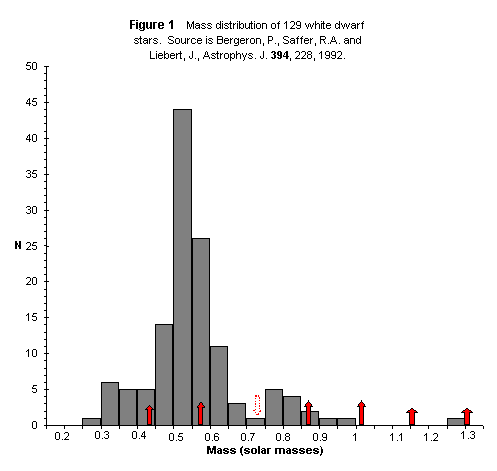
Notable in Figure 1 is the significant “gap” in the 0.70 M8 – 0.75 M8 bin, a dominant peak near the expected value of 0.58 M8 and a low-mass shoulder in the region of 0.4 M8.
FIGURE
2
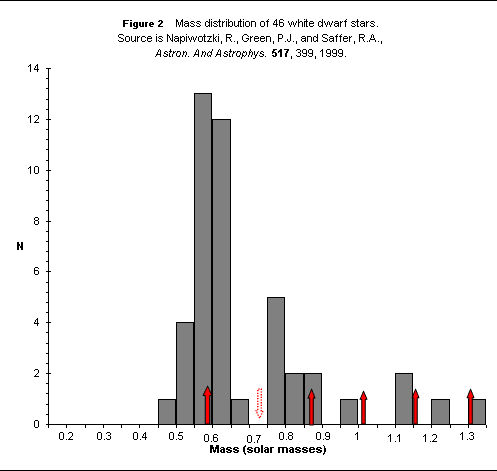
The sample in Figure 2 is quite small, but the observed distribution is reasonably consistent with the predicted one.
FIGURE
3
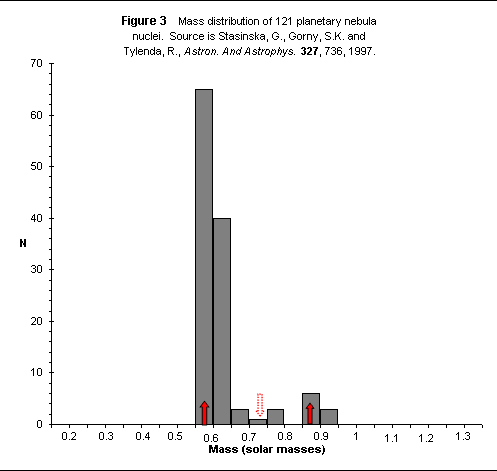
Figure 3 is a sizeable sample of PNN that has a dominant peak at » 0.58 M8, a much smaller peak at » 0.87 M8 and the expected valley between them.
FIGURE
4
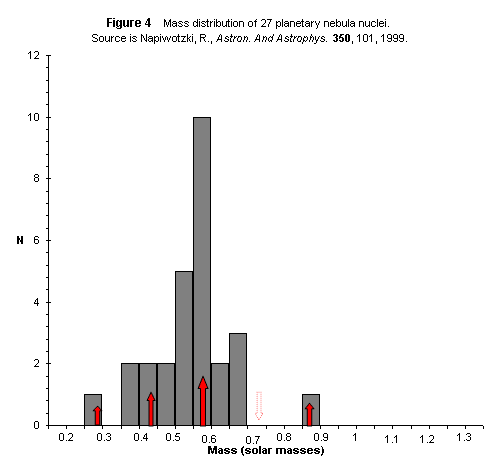
Figure 4 is a small sample of PNN that looks much like Figure 3, but with a clear shoulder at » 0.44 M8.
FIGURE
5
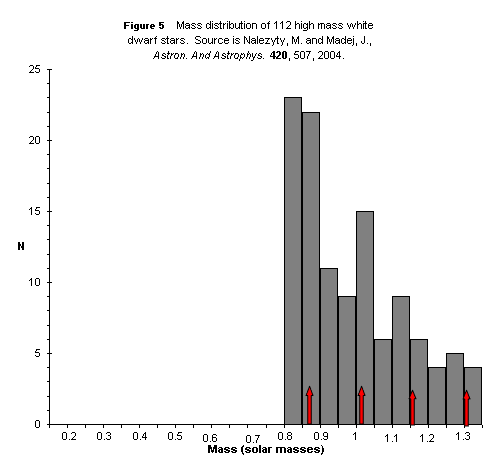
Figure 5 displays a sample of high-mass WDs (M ≥ 0.80 M8) that is consistent with the expected peaks at » 0.87 M8, » 1.02 M8 and possibly » 1.16 M8.
In Figure 6 we combine the samples of Figures 1-5 in the hope of achieving a large sample that minimizes any small systematic errors in the individual samples.
FIGURE
6
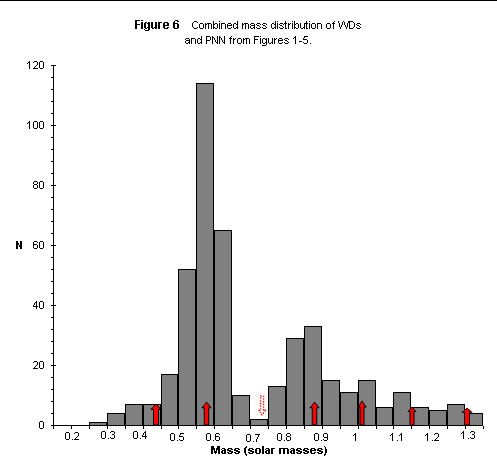
Although the rectitude of crudely lumping these samples together can certainly be questioned, the results are fairly impressive and speak for themselves.
A recent reanalysis of the WD masses from the Palomar Green Survey is shown in Figure 7.
FIGURE
7
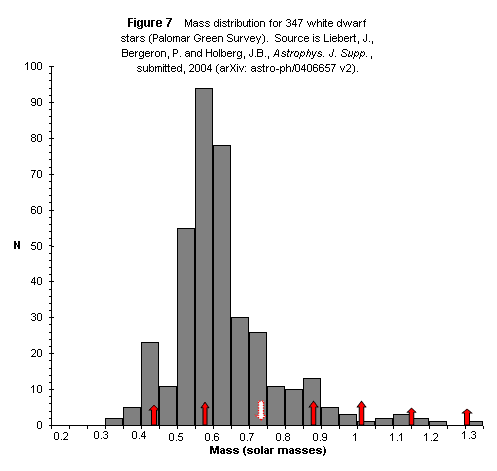
Notable in this sample is the distinct peak in the 0.40 M8 – 0.45 M8 bin, and the disappearance of the “gap” at » 0.73 M8
FIGURE
8
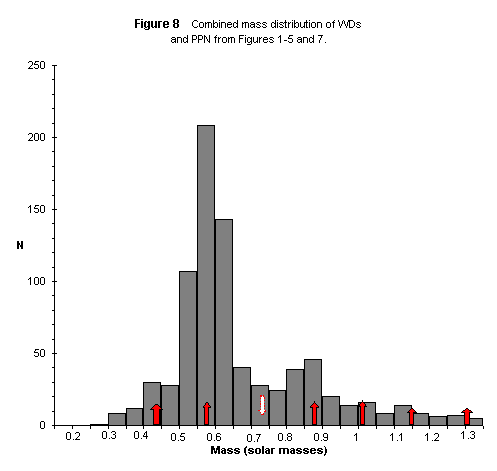
When the Palomar Green results are added to the combined sample of Figure 6, we get a large sample (Figure 8) that meets most of our expectations. Predicted peaks at » 0.44 M8, » 0.58 M8 and » 0.87 M8 are clearly present, and the high-mass tail of the distribution has small peaks at » 1.02 M8 and » 1.16 M8. There is a shallow valley between 0.70 M8 and 0.80 M8, although not the pronounced “gap” that was seen in Figure 6.
Anticipating an interest in whether samples of other classes of stars indicate preferences for the predicted mass peaks discussed above, Figure 9 is offered.
FIGURE
9
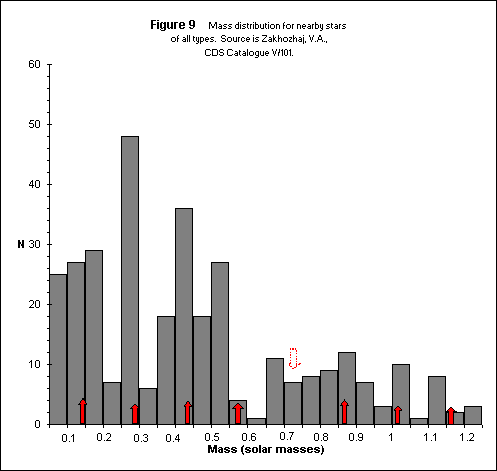
This sample is comprised of stars that are classified as “nearby” (within 10 parsecs of the Sun), and therefore is a mixture of different types of stars, mostly main sequence stars. There is good agreement between the red arrows and the peaks in the sample, except for the region of 0.55 M8 to 0.80 M8.
Interestingly, the agreement between Figure 9 and the predicted stellar mass distribution is weakest in the region where the agreement is strongest for the WD and PNN samples.
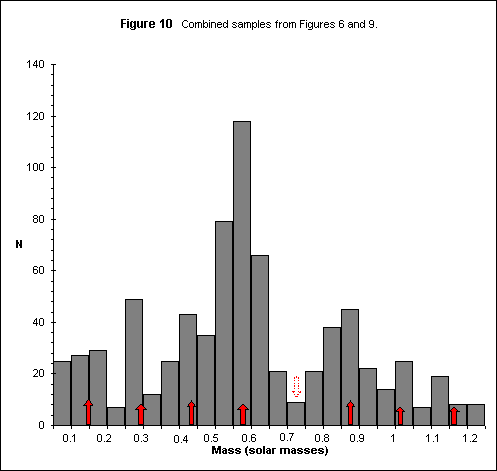
Although the legitimacy of combining these very different samples is in serious doubt, Figure 10 shows what happens when this is done.