 |
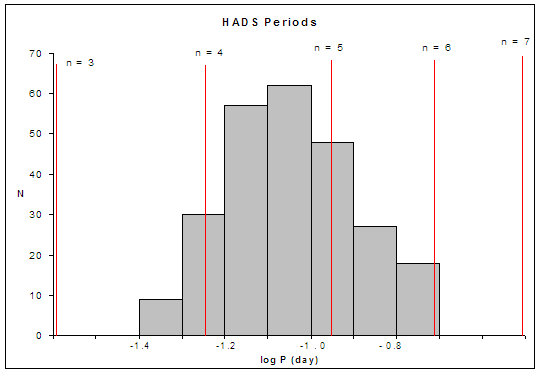
Figure 1. Histogram of periods for 193 high amplitude δ Scuti stars.2 Superimposed upon the period distribution are lines representing the scaled oscillation periods for Rydberg atoms excited to various n values. |
This “New Development” builds upon the results obtained in its predecessor, which discussed the discrete fractal behavior of RR Lyrae variables. For that class of stars, it was demonstrated that the masses, radii and oscillation periods of RR Lyraes have a discrete self-similar relationship to the masses, radii and transition periods of their Atomic Scale counterparts: helium atoms in moderately excited Rydberg states undergoing single-level transitions. The techniques that were used to achieve this unique result are now applied to a distinctly different class of variables: δ Scuti stars. The new results contain some interesting surprises, but they are in general agreement with the discrete fractal paradigm and offer additional supportive evidence for the principle of discrete cosmological self-similarity.
The presentation given here assumes a basic understanding of the SSCP (see Paper #1 in the “Selected Papers” section of this website) and a familiarity with the previous “New Development” (see “RR Lyrae Stars, Helium Atoms And Energy State Transitions” – Sept 2005).
At critical points in this presentation we will rely on our trusty discrete scale transformation equations:
R = Λr , (1)
P = Λp and (2)
M = ΛD m , (3)
where R, P and M are radii, periods and masses of Stellar Scale systems and r, p and m are the equivalent parameters for their Atomic Scale counterparts. As before, Λ and D are dimensionless self-similar scaling constants with values of ≈ 5.2 x 1017 and ≈ 3.174, respectively. The numerical value of ΛD is ≈ 1.70 x 1056.
Compared with RR Lyrae stars, δ Scutis are a somewhat unruly lot. For example, the amplitudes of their oscillation periods can vary radically. As Breger and Pamyatnykh1 point out: “A star may change its pulsation spectrum to such an extent as to appear as a different star at different times”, although “modes do not completely disappear, but are still present at small amplitudes.” Here we will exclusively work with high amplitude δ Scuti stars (HADS) because their pulsation behavior is simpler (less multi-periodic) and more regular than low amplitude δ Scutis (LADS), and because they are thought to pulsate mainly in radial modes,2 which helps in identifying specific energy level transitions. Delta Scutis have spectral classifications of A to F and can be designated dwarf or subgiant stars.3 Most importantly, their masses4 typically range from 1.5 M¤ to 2.5 M¤. This is a major change from the situation with the RR Lyrae class wherein the lower, narrower and better-defined mass range was 0.4 M to 0.6 M¤.
As of 2004 roughly 400 δ Scutis were known. A typical oscillation period would be 0.1 day, and the cutoffs for this class occur at roughly 0.04 day and 0.2 day. In Figure 1 we show a representative histogram of oscillation periods for 193 HADS.2 Superimposed upon this distribution are lines corresponding to typical oscillation periods for Stellar Scale n values, which will be derived and explained below.
 |
Figure 1. Histogram of periods for 193 high amplitude δ Scuti stars.2 Superimposed upon the period distribution are lines representing the scaled oscillation periods for Rydberg atoms excited to various n values. |
In this particular sample of 193 HADS stars, there were 40 double-mode pulsators and twelve stars that simultaneously pulsed at 3 or more periods. Unfortunately, data on the radii of HADS stars appear to be very limited; this causes a minor problem with regard to identifying relevant energy levels, but the problem can be circumvented.
Given Eq. (3) and the mass of the proton (mp), we can calculate that the Stellar Scale proton analogue will have a mass of about 0.145 M¤. The mass range (1.5 M¤ – 2.5 M¤) for δ Scuti stars would correspond to an Atomic Scale mass range of approximately 10 mp to 17 mp, or about 10 – 17 atomic mass units (amu). The atoms that dominate this mass range are Boron (11 amu), Carbon (12 amu), Nitrogen (14 amu) and Oxygen (16 amu). Therefore the majority of δ Scuti stars are hypothesized to be analogues of these atoms. Because reliable radius data are not available, an alternative method must be derived for determining the approximate energy levels of the relevant Atomic Scale transitions. There is a general relationship between the radial quantum numbers (n) for Rydberg atoms and their oscillation periods of the form:
pn ≈ n3po , (4)
where po is the classical orbital period of the groundstate H atom:≈ 1.5 x 10-16 sec. The Stellar Scale equivalent to this relationship would be:
Pn ≈ n3Po , (5)
where
The above considerations lead us to conclude that δ Scuti variables correspond to a very heterogeneous set of B, C, N and O atoms excited to Rydberg states with n approximately varying between 3 and 6. The next step is to test this hypothesis by comparing the oscillation periods of δ Scuti stars with specific oscillation periods of their predicted Atomic Scale counterparts. However, there is a serious problem with a straightforward comparison between Stellar Scale and Atomic Scale frequency/period spectra, as was possible in the case of the RR Lyrae class. The main source of this problem is the heterogeneity of the δ Scuti class of stars. We are dealing with analogues of at least four different atoms, each of which can be in several different isotopic configurations. Moreover, each of those four species of atom can be in several different ionization states: -1, neutral, +1, +2, etc. A further complication is that each of the atoms can have an entirely different set of energy levels for each of the singlet, doublet, triplet, etc., spin-related designations that apply. Also, we are less confident about using the Δn ≈ 1 and l ≤ 1 restrictions that were so helpful in the RR Lyrae case. Therefore, we are faced with a very large number of potential Atomic Scale transition periods to compare with the δ Scuti period distributions. A meaningful test requires that the number of Stellar Scale periods should not be outnumbered by the experimental Atomic Scale periods with which they are to be compared. In the case of the δ Scuti class of stars, the number of empirical comparison periods would be in the hundreds, exceeding the number of observed HADS periods! Compounding this general lack of Atomic Scale specificity are the usual uncontrollable physical factors that can result in additional shifting of Stellar Scale energy levels away from unperturbed values: ambient pressures, temperatures, electric fields and magnetic fields.
Fortunately, there is a way to circumvent the alarming specificity problems discussed above. If we have enough accurate information for an individual δ Scuti star, then we can use the data to identify the specific Atomic Scale analogue of the star, to restrict the number of possible energy level transitions for that specific atom, and to construct a valid test between a uniquely predicted oscillation period and a reasonably restricted number of Atomic Scale comparison periods. Very recently, the δ Scuti star GSC 00144–03031 was analyzed in detail by Poretti et al5 and this system has certain characteristics that make it an excellent test star for our purposes. First and foremost, its mass has been determined with reasonable accuracy and is approximately 1.75 M. Using our knowledge that 0.145 M¤ ≈ 1 SMU (Stellar Mass Unit) ≈ ΛD amu (atomic mass units) ≈ ΛDmp, we can determine that 1.75 M¤ corresponds to 12 SMU and therefore GSC 00144–03031 can be identified with a high degree of confidence as an analogue of a 12C atom. Other advantages of using this star as a test system are that it is a classic HADS system (regular, high amplitude pulsations), that it has a dominant fundamental mode that is highly radial in character (which helps in narrowing energy level possibilities), and finally that it is a pure double-mode pulsator (providing us with an second test period). The fundamental radial mode has a period of about 0.058 day (≈ 83.6 min or ≈ 5017.42 sec) and its amplitude is 4 times greater than the secondary pulsation which has a period of ≈ 3872.70 sec.
Table 1. Physical Properties of GSC 00144–030315
Class |
|
Mass |
≈ 1.75 M¤ |
Mode |
“pure double-mode pulsator” with radial fundamental mode |
Fundamental Period |
5017.42 sec (radial, amplitude = 0.1383 mag) |
Secondary Period |
3872.70 sec (amplitude = 0.0331mag) |
If the principle of discrete cosmological self-similarity is correct, then we should be able to use the oscillation periods of GSC 00144-03031 to derive predicted oscillation periods for comparison with empirical oscillation periods of its Atomic Scale analogue undergoing corresponding transitions. We have identified the Atomic Scale analogue as a 12C atom and the transition has a strong radial mode (l = 0) character. From Figure 1, we can determine that the position of the dominant period for GSC 0144–03031 falls between the n ≈ 5 and the n ≈ 4 lines and so we anticipate a n = 5 → 4 (low l) transition. Using Eq. (2) we can calculate the predicted Atomic Scale period:
p ≈ P ÷ Λ ≈ 5017.42 sec ÷ 5.2 x 1017 ≈ 9.65 x 10-15 sec.
We assume that the 12C atom is most likely to be in a neutral, rather than an ionized, state. Therefore the quantitative test is whether a neutral 12C atom has a radial mode transition between the n = 5 and n = 4 levels that involves an oscillation period of about 9.65 x 10-15 sec. We use a standard source for atomic energy level data6 and find that the n = 5 energy level with the least non-radial character is the 1s22s22p5p(J=0) 1S singlet level with an energy of 85625.18 cm-1. The n = 4 energy level with the least non-radial character is the 1s22s22p4p(J=0) 1S singlet level with an energy of 82251.71 cm-1. Subtracting the energies for these neighboring energy levels gives 3373.47 cm-1 as the transition energy (ν) for the n = 5(J=0) → n = 4(J=0) transition. We can calculate the oscillation period for the transition by using the relation ν = νc for electromagnetic radiation, and we find that ν = (3373.47 cm-1)(2.99 x 1010 cm/sec) = 1.01 x 1014 sec-1. Since p = 1/ν, the period for the transition is 9.88 x 10-15 sec. This value is higher than the predicted value of 9.65 x 10-15 sec by a factor of 0.024, but considering the numerous sources of small uncertainties that are involved in this test, and the uncontrollable physical factors that can shift the Stellar Scale oscillation period, the agreement between the predicted and experimental values is quite good. Table 2 summarizes the discrete self-similarity between GSC 00144–03031 and 12C [1s22s22p5p → 4p, (J=0), 1S].
Table 2. Comparison of the Fundamental Mode Properties of GSC 00144–03031 and Its 12C Analogue Undergoing a [1s22s22p5p(J=0) → 4p(J=0), 1S] Transition
Parameter |
GSC 00144-03031 | Scale Factor |
Predicted Analogue Values | Empirical 12C values |
Error |
Mass |
1/ΛD |
-
|
|||
Fund. Mode |
radial |
≈ radial |
0
|
||
n |
- |
4 < n < 5 |
4 < n < 5 |
0
|
|
Period |
5017.42 sec |
1/Λ |
9.65 x 10-15 sec |
9.88 x 10-15 sec |
0.024
|
To check on the uniqueness of the discrete self-similar relationship between the specific oscillation periods of GSC 00144–03031 and 12C [5p(J=0) → 4p(J=0), 1S], the oscillation periods of other transitions in the 3 ≤ n ≤ 5 range were checked. The closest alternative match occurred for the [5p(J=2) → 4p(J=2), 1D] transition. However, its oscillation period (9.18 x 10-15 sec) is about 5% low and the transition is not similar to a fundamental radial mode oscillation. Oscillation periods for other 12C transitions [3 ≤ n ≤ 5; 1S and 3S] differed from the predicted period of 9.65 x 10-15 sec by 10% or more. Given the good quantitative match between the fundamental period of GSC 00144–03031 and the single uniquely specified transition period of 12C, it seems fair to conclude that discrete cosmological self-similarity has been shown to apply in this case.
To further demonstrate the uniqueness of our result, we can repeat the same analysis for other atoms such as H, He, Li, Be, B and N. The results of these calculations are summarized in Table 3.
Table 3. Oscillation Periods [5(l ≈ 0) → 4(l ≈ 0)] for Atoms Other Than 12C
Atom |
DE (cm-1) |
p (sec) |
H |
2467.78 |
1.35 x 10-14 |
He |
2723.28 |
1.22 x 10-14 |
Li |
3287.47 |
1.02 x 10-14 |
Be |
4076.88 |
8.18 x 10-15 |
B |
5136.47 |
6.49 x 10-15 |
N |
4583.11 |
7.27 x 10-15 |
Although at present we do not have enough information to definitively choose between the three candidate matches for the secondary oscillation of GSC 00144–03031, we can safely say that this additional check on the uniqueness of the primary results for the dominant oscillation period yields confirmatory results. Had we not found any period matches at the ≤ 5% level, then that might have indicated a serious problem with the analysis, or possibly with the whole concept of discrete cosmological self-similarity.
The class of δ Scuti variable stars is a much more heterogeneous class than the RR Lyrae class, corresponding to a collection of Atomic Scale systems with masses in the 10-17 amu range. The high amplitude δ Scuti stars appear to be limited to low Δn transitions (ni – nf ≈ 1) primarily within the range 3 ≤ n ≤ 6. The substantial heterogeneity of this class interferes with a simple comparison of sizeable samples of δ Scuti oscillation periods with predicted periods derived from Atomic Scale data, although this is possible in principle. However, we have achieved the specificity required for a meaningful test of discrete cosmological self-similarity by focusing on an individual, well-characterized δ Scuti star. The success in predicting: (1) a specific Atomic Scale analogue (12C), (2) a most likely transition (1s22s22p5p → 4p, J=0, 1S) and (3) a correct oscillation period (to < 3%), based purely on physical data for GSC 00144–03031, combined with the previous successful demonstration of discrete self-similarity between RR Lyrae stars and He atoms undergoing Dn = 1 transitions between Rydberg states, lends further support to our contention that discrete cosmological self-similarity is a fundamental property of nature. These successes also lead us to predict that the same methods that have been applied here, and in the case of the RR Lyraes, can be successfully applied to other δ Scuti stars if the following criteria are met. The stellar mass must be known to an accuracy of ≤ 0.05 M¤, so that the correct Atomic Scale analogue can be identified. Ideally the star should pulsate in a single dominant oscillation mode, although double-mode pulsators can also be analyzed by our methods. Multi-mode pulsators with three or more low amplitude periods appear to be analogous to excited, highly perturbed, atomic systems that are oscillating at several potential transition periods, but are not yet undergoing single specific transitions between energy levels, as will be discussed in the next “New Development” on the class of ZZ Ceti variable stars. At any rate, the higher the amplitude of the dominant oscillation period of the δ Scuti star, the more likely it is that we are observing an event that is self-similar to a full-fledged transition between discrete energy levels. Although we may be getting a bit ahead of ourselves here, it is conceivable that a typical single-mode HADS star evolves from a multi-mode LADS star when the latter absorbs a sufficient amount of energy at an appropriate frequency in order to trigger a genuine energy level transition.
If you like solving puzzles, you might enjoy the challenge of identifying a well-studied δ Scuti variable and using the above methods to determine its self-similar counterpart on the Atomic Scale.
1. Breger, M. and Pamyatnykh, A.A., preprint, arXiv:astro-ph/0509666 v1, available at http://www.arXiv.org, 2005
INTRODUCTION
In papers #1 and #2 of the “Selected Papers” section of this website, variable stars such as RR Lyrae and Cepheid stars were identified as Stellar Scale analogues of excited atoms undergoing transitions between discrete energy levels. At the time that those papers were written only rough tests of the qualitative and quantitative self-similarity between the proposed stellar and atomic analogues were attempted. Here we will refine the case for a remarkable degree of self-similarity between RR Lyrae stars and one of their major constituents: excited helium atoms undergoing single-level transitions involving s and p states.
The discrete self-similar scaling equations used throughout this website will play a key role in our investigation. They are:
Rn = ΛRn-1 , (1)
Tn = ΛTn-1 and (2)
Mn = ΛD Mn-1 , (3)
where R, T and M are spatial lengths, temporal “lengths” and masses of analogue systems on neighboring cosmological Scales n and n-1, and where Λ (≈ 5.2 x 1017) and D (≈ 3.174) are dimensionless scaling constants. For the specific case at hand, we may rewrite these self-similar transform equations in a more convenient format:
R = Λr , (4)
P = Λp and (5)
M = ΛD m , (6)
where it is understood that capital letters denote Stellar Scale radii, periods and masses, while lower case letters refer to the counterpart parameters of Atomic Scale analogues.
We will see that there appears to be a one-to-one correspondence between
the qualitative properties of RR Lyrae stars and excited helium atoms undergoing
single-level transitions. Furthermore, their quantitative properties
such as sizes, masses and oscillation periods obey our discrete self-similar
scaling equations quite accurately. Individual peaks in RR Lyrae period
distributions are shown to correspond to specific 4He transition
periods. Inherent and practical observational uncertainties that place
limits on the quantitative exactitude with which we can test the true degree
of self-similarity will be discussed.
RR LYRAE VARIABLE STARS
We choose
RR Lyrae stars for this test of the Principle of Cosmological Self-Similarity
because this class of variable stars is particularly homogeneous
in terms of masses, periods, amplitudes, modes, and light curves.1,2 This
helps to insure that the confusing influence of Stellar Scale analogues
of more massive atoms in He-like singly excited states is minimized. RR
Lyrae stars are blue giant stars with classifications of A or F. There
are three main subtypes designated RRa, RRb and RRc with typical
periods1 of
0.5 days, 0.7 days and 0.3 days. The full period range1,2 for
RR Lyraes is roughly 0.2 days to 1.0 days. Typical radii3 for
RR Lyrae variables range from about 3.7 R¤ to
roughly 7.2 R¤,
and their masses have been estimated1,2 in the range: 0.43 M¤ to
0.65 M¤, with ≈ 0.6
M¤ being the most
typical value.
TABLE 1 BASIC PROPERTIES OF RR LYRAE STARS
Subtype |
<Period> |
<Amplitude> |
Light Curve Shape |
RRa |
~ 0.5 days |
~ 1 mag |
sharp, asymmetric |
RRb |
~ 0.7 days |
~ 0.5 – 0.8 mag |
intermed. asymm. |
RRc |
~ 0.3 days |
~ 0.5 mag |
almost sinusoidal |
Figure 1 shows a typical period distribution for RR Lyrae stars; the data4 are from the globular cluster IC 4499. There are three major peaks that roughly correspond to the three subtypes. Much larger samples of RR Lyrae periods from a recent catalog will be shown and discussed in detail later in this presentation.
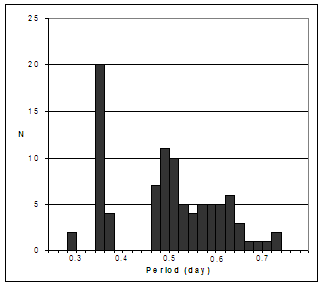
FIGURE 1 Histogram of periods4 for RR Lyrae stars in IC 4499.
The majority of RR Lyrae stars are believed to pulsate in the fundamental radial mode (spherical expansion and contraction), and their radii at maximum expansion tends to be about 10% greater than their radii at full contraction.2 The stars' luminosity is inversely proportional to its size during the oscillations. It has been “definitely established” that the pulsations occur in the outer envelopes of the stars, rather than in their cores.2
ATOMIC SCALE ANALOGUES OF RR LYRAE STARS
We begin our search for self-similar Atomic Scale analogues of RR Lyrae variables with a fundamental and diagnostic property: the mass of the systems. Given the typical or average mass for RR Lyraes: <M> ≈ 0.6 M¤, we may use Eq. 6 to calculate the corresponding <m> value for the appropriate Atomic Scale analogue.
<m> ≈ (0.6 M¤)(1.99 x 1033 g/M¤) ¸ (5.2 x 1017)3.174
≈ 7.0 x 10-24 g
The mass of the 4He atom is about 6.7 x 10-24 g and this is within 4.8 % of the rough estimate derived from <M>. The fact that M may go as low as 0.43 M¤, which is ≈ ¾ <M>, suggests that small numbers of 3He analogues may be found in RR Lyrae populations.
Given the range of radii for RR Lyrae stars and equation 4, we can calculate the equivalent radius range for the Atomic Scale analogues.
<r>lower ≈ (3.7 R¤)(6.96 x 1010 cm/R¤) ¸ 5.2 x 1017 ≈ 4.95 x 10-7 cm
<r>upper ≈ (7.2 R¤)(6.96 x 1010 cm/R¤) ¸ 5.2 x 1017 ≈ 9.64 x 10-7 cm
Using the general relationship5 between the radial quantum number (n) and radius (r) for Rydberg atoms (ground state core + single excited electron) in states with low angular quantum number (l ):
r ≈ 2n2ao ,
where ao is the Bohr radius (≈ 0.529 x 10-8 cm), we can get a rough estimate of the range of n values that apply to the Atomic Scale analogues of RR Lyrae stars as follows.
nlower ≈ (rlower/2ao)1/2 ≈ (4.95 x 10-7cm/1.058 x 10-8 cm)1/2 ≈ 6.8
nupper ≈ (rupper/2ao)1/2 ≈ (9.64 x 10-7 cm/1.058 x 10-8 cm)1/2 ≈ 9.5
Since most RR Lyrae stars are believed to oscillate in the fundamental
radial mode (l = 0), their Atomic
Scale analogues would primarily involve s-states with l = m = 0.
AN IMPORTANT TEST
Now we are ready for an important test of the proposed analogy between
RR Lyrae stars and singly excited 4He atoms undergoing single-level
energy transitions. If there is true self-similarity between the proposed
analogues, then 4He atoms undergoing transitions between 1sns
states (with n = 7-10) should have oscillation periods that are quantitatively
related to the RR Lyrae star oscillation periods in the manner specified
by Eq. 5. Table 2 provides the data6 needed for this test,
including initial (i) and final (f) values of n, transition energies,
Atomic Scale transition periods and predicted Stellar Scale oscillation periods
for self-similar analogues. Single level transitions for singlet (1S)
and triplet (3S) states are listed for 4He (1sns) with
n = 1-15. Also shown for comparison purposes are several multi-level
transitions within the relevant range of 1sns states.
TABLE 2 TRANSITION DATA FOR 4He (1snis → 1s[ni -1]s)
ni → nf ; xS |
DE (atomic units) |
Atomic Scale Transition Period (sec) |
Predicted Stellar Scale Oscillation Period (day) |
2 – 1; 3S |
0.72850 |
2.0857 x 10-16 |
0.0013 |
3 – 2; 3S |
0.10654 |
1.4260 x 10-15 |
0.0086 |
4 – 3; 3S |
0.03218 |
4.7220 x 10-15 |
0.0284 |
5 – 4; 3S |
0.01389 |
1.0939 x 10-14 |
0.0658 |
6 – 5; 3S |
0.00724 |
2.0980 x 10-14 |
0.1263 |
7 – 6; 3S |
0.00425 |
3.5768 x 10-14 |
0.2153 |
8 – 7; 3S |
0.00270 |
5.6275 x 10-14 |
0.3387 |
9 – 8; 3S |
0.00183 |
8.3029 x 10-14 |
0.4997 |
10 – 9; 3S |
0.00129 |
1.1778 x 10-13 |
0.7089 |
11 – 10; 3S |
0.00100 |
1.5194 x 10-13 |
0.9145 |
12 – 11; 3S |
0.00066 |
2.3022 x 10-13 |
1.3855 |
13 – 12; 3S |
0.00055 |
2.7526 x 10-13 |
1.6566 |
14 – 13; 3S |
0.00044 |
3.4849 x 10-13 |
2.0974 |
15 – 14; 3S |
0.00035 |
4.3412 x 10-13 |
2.6128 |
2 – 1; 1S |
0.75775 |
2.0052 x 10-16 |
0.0012 |
3 – 2; 1S |
0.08470 |
1.7938 x 10-15 |
0.0108 |
4 – 3; 1S |
0.02769 |
5.4885 x 10-15 |
0.0330 |
5 – 4; 1S |
0.01241 |
1.2244 x 10-14 |
0.0737 |
6 – 5; 1S |
0.00661 |
2.2973 x 10-14 |
0.1383 |
7 – 6; 1S |
0.00394 |
3.8583 x 10-14 |
0.2322 |
8 – 7; 1S |
0.00253 |
6.0056 x 10-14 |
0.3614 |
9 – 8; 1S |
0.00172 |
8.8339 x 10-14 |
0.5317 |
10 – 9; 1S |
0.00123 |
1.2353 x 10-13 |
0.7435 |
11 – 10; 1S |
0.00090 |
1.6827 x 10-13 |
1.0127 |
12 – 11; 1S |
0.00068 |
2.2212 x 10-13 |
1.3369 |
13 – 12; 1S |
0.00053 |
2.8612 x 10-13 |
1.7222 |
14 – 13; 1S |
0.00042 |
3.6088 x 10-13 |
2.1721 |
15 – 14; 1S |
0.00034 |
4.4822 x 10-13 |
2.6975 |
10 – 8; 1S |
0.00295 |
5.1496 x 10-13 |
0.3099 |
9 – 7; 1S |
0.00426 |
3.5699 x 10-14 |
0.2149 |
8 – 6; 1S |
0.00647 |
2.3486 x 10-14 |
0.1414 |
10 – 7; 1S |
0.00548 |
2.7712 x 10-14 |
0.1668 |
The predicted Stellar Scale periods are calculated in the following manner. From a table6 of energy levels corresponding to 4He (1sns), we subtract Ei from Ef to get DE for the transition. These data are usually given in atomic units (au) which can be converted to electron-volts (ev) by multiplying by 27.2 ev/au. Since DE = hn, where h is Planck’s constant, we can calculate the frequency n for the transition. Then, p = 1/n and P = Λp. Data for the relevant range of n values are highlighted in Table 2.
The results presented in Table 2 are very encouraging. The predicted
Stellar Scale oscillation periods derived from 4He atoms undergoing
1s8s → 1s7s transitions are 0.3387
days and 0.3614 days for the triplet (3S) and singlet (1S)
state transitions, respectively. For the 1s9s → 1s8s
transitions we derived predicted periods of 0.4997 days and 0.5316 days. For
the 1s10s → 1s9s transitions
the predicted Stellar Scale periods are 0.7089 days and 0.7435 days. These
three period ranges: ≈ 0.35
days, ≈ 0.51 days and ≈ 0.72 days correspond quite well to
typical periods of ≈ 0.3
days, ≈ 0.5 days and ≈ 0.7 days for RRc, RRa and RRb variables, respectively. The
derived Stellar Scale periods for the 1s7s → 1s6s
transitions are 0.2153 days and 0.2322 days, which corresponds well with
the lower limit of ~ 0.2 days for
RR Lyrae stars. The predicted periods for analogues to the 1s11s → 1s10s transitions of helium are 0.9145
days and 1.0127 days, which corresponds well with the upper limit of ~ 1.0 days for RR Lyrae stars. Given
this level of agreement between the masses, radii, periods and qualitative
properties (oscillating spherical systems with pulsations taking place in
the outer envelopes), I think one is justified in claiming that a considerable
degree of self-similarity has been demonstrated between RR Lyrae stars and 4He
atoms undergoing 1sns transitions with n ≈ 7-10
and Dn = 1. Below we will show
that the case for this example of stellar/atomic self-similarity can be made
even stronger, but first we need to acknowledge some observational limitations.
DISCRETE VERSUS CONTINUOUS PERIOD DISTRIBUTIONS
One might argue that while the self-similarity discussed above is interesting, it would not extend to more detailed comparisons of the period distributions for atoms undergoing de-excitations and variable stars. When we think of Atomic Scale transition spectra we tend to envision them as rigorously discrete, with unique well-separated peaks or even narrow lines. Variable stars, on the other hand, may manifest preferred period ranges but they have much broader, and seemingly continuous, period distributions. Actually this apparent disparity between the Atomic Scale and Stellar Scale analogues may be quite misleading. Discrete atomic spectra are achieved by carefully limiting the observations to an extremely homogeneous sample of atoms undergoing a small number of specific state transitions, with strict control over ambient electric fields, magnetic fields, pressures, temperatures and sources of contamination. When we observe clouds of interstellar matter, wherein the capacity for experimental manipulation is severely limited, then we see quasi-continuous frequency distributions with “preferred” peaks, much like those seen for variable stars.
Consider the following list of physical factors that tend to obscure the discreteness of atomic spectra by shifting the energy levels, and the related transition periods, from their unperturbed positions, or by the addition of “foreign” systems with their extraneous transition periods.
1. 1S and 3S states: Each 1sns energy level for 4He has two values, one for a singlet state and another for a triplet state (see any quantum mechanics text for a discussion of this spin-related phenomenon). Therefore each transition period gets split into a pair of transition periods.
2. l > 0; -l ≤ m ≤ +l states: If some systems with l = 1 (or higher) are present, but are assumed to be in l = 0 states, then additional transition periods will “contaminate” the observations. For l > 0 we also have multiple sets of spurious transition periods due to the fact that the magnetic quantum number (m) can be equal to any whole number between –l and +l.
3. Electric fields: Because of their substantial charge separation, Rydberg atoms are significantly effected by ambient electric fields, which shift energy levels and transition periods.
4. Magnetic fields: Rydberg atoms are also strongly affected by ambient magnetic fields, which also lead to shifts in energy levels and transition periods.
5. Temperature and pressure: The positions of energy levels can be shifted by ambient temperatures and pressures, which can be quite high in astrophysical settings.
6. Contaminants: Atoms other than helium but with electronic configurations like that of He (1sns), such as Li+ (1sns) and H- (1sns), will each add extraneous sets of transition periods.
7. Isotopes of He: To the extent that 3He and 6He isotopes contaminate the 4He test sample, additional sets of transition periods will be present.
8. Dn > 1: Some of the 4He atoms undergoing 1snis → 1snfs transitions may have ni – nf > 1 and will contribute spurious transition periods to the relevant period distribution for ni – nf = 1 transitions.
No doubt this is only a partial listing of the many physical factors that
can lead to a virtual “forest” of transition periods. In
the modern laboratory we can control these factors and observe very discrete
spectra. When we cannot control these factors, such as when we observe
the spectra of interstellar atoms or the period distributions of variable
stars, then we should not be surprised to find quasi-continuous distributions
of transition periods. There will be a tendency for preferred peaks
at recognizable positions, but these peaks may sometimes be shifted. This
is a very important point. A failure to acknowledge these realities
might cause us to seriously underestimate the true degree of cosmological
self-similarity and the value of stellar/atomic analogies.
MORE RR LYRAE “SPECTRA”
With the lessons of the immediately preceding paragraphs in mind, we are ready to take a more diagnostic look at some recently observed period “spectra” for large numbers of RR Lyrae stars. One of the secondary benefits of various gravitational microlensing experiments, whose primary goal is to prove or falsify the hypothesis that the ubiquitous galactic dark matter is in the form of stellar-mass dark objects, is the detection of large numbers of variable stars. Recently the Optical Gravitational Lensing Experiment (OGLE) team published a RR Lyrae catalog7 with data on 7612 of these variable stars that are located in the Large Magellanic Cloud (LMC). The OGLE team has prepared period distribution histograms using narrow binning and and multiple-binning analyses that produce particularly detailed and accurate period distributions.
Figure 2 shows the period distribution for the full sample of 7612 LMC RR Lyrae variables, with the stars divided into five categories: RRab, RRc, RRd (double-mode), RRe (2nd overtone) and “other”.
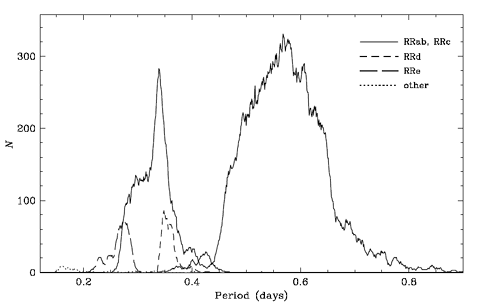
FIGURE 2 Histogram of periods for RR Lyrae stars in the LMC.7
There is a very sharp peak for the RRc subset, and the “most likely
period of RRc variables is equal to <Pc> = 0.339 days,” which
is virtually identical to the predicted Stellar Scale analogue of
the 4He
1s8s → 1s7s (3S) transition
period: 0.3387 days. On the other hand, there is a small but fairly
well-defined sub-peak of RRe stars with <Pe> = 0.28 days,
which does not seem to correlate well with one of our six predicted
periods for li = lf = 0. Since RRe stars are thought to be “2nd overtone” (l > 0)
pulsators, we are probably dealing with analogues to transitions
that involve p-states. The additional transitions most likely to be
relevant to our study are single-level transitions between p-states
and s-states with n values in the previously specified range of 10 ≥ n ≥ 7. Therefore
we present Table 3 with the appropriate transitions and derived period
predictions.
TABLE 3 TRANSITION DATA FOR 4He (1snip – 1s[ni-1]s)
ni → nf; xS |
DE (atomic units) |
Atomic Scale Transition Period (sec) |
Predicted Stellar Scale Oscillation Period (days) |
10p – 9s; 1S |
0.00138 |
1.0991 x 10-13 |
0.6615 |
9p – 8s; 1S |
0.00194 |
7.8446 x 10-14 |
0.4722 |
8p – 7s; 1S |
0.00284 |
5.3559 x 10-14 |
0.3223 |
10p – 9s; 3S |
0.00153 |
9.9130 x 10-14 |
0.5966 |
9p – 8s; 3S |
0.00216 |
7.0340 x 10-14 |
0.4233 |
8p – 7s; 3S |
0.00318 |
4.7725 x 10-14 |
0.2872 |
We now have a set of 12 predicted RR Lyrae periods that correspond to the full set of single-level transitions for 4He atoms with 10 ≥ n ≥ 7 and 0 ≤ l ≤ 1. With this expanded set of predicted periods, we are ready to take a second look at Figure 2.
We recall that there is an excellent match between the main RRc peak and the 1s8s → 1s7s (3S) transition. The RRe peak at 0.28 days can now be understood as a self-similar analogue to the 1s8p → 1s7s (3S) transition for 4He. The shorter period of the RRd subset has a sharp peak at 0.35 days and its period distribution is centered at 0.36 days, which is in good agreement with the predicted period derived from the 1s8s → 1s7s (1S) transition: 0.3614 days. There is a very broad shoulder to the left of the main RRc peak which may be largely due to a sizeable contribution from the 1s8p → 1s7s (1S) transition analogue with a predicted period of 0.3223 days, and possibly a contribution from the 1s10s → 1s8s (1S) transition at 0.3099 days. Note the dramatic valley in the period distribution between 0.38 days and 0.45 days, which is in very good agreement with the predicted gap between the various n = 8 → 7 transitions and the longer period (n = 9 → 8; n = 10 → 9) transitions. A “blip” centered at about 0.425 days may correspond to the 1s9p – 1s8s (3S) transition at 0.4233 days, while the other “blip” at about 0.4 days has not yet been identified.
Moving now to the RRab subset, we immediately see one of the drawbacks of large samples: an embarras de richesses. We have good reason to suspect that this huge “single” peak is in actuality a composite of many much more narrow peaks, but the resolution is not sufficient to give more than a hint of the underlying substructure. All we can safely say is that the sharp rise beginning at ≈ 0.45 days, the jagged top, the approximate mid-peak location, and the sharp drop-off beyond 0.65 days meet our expectations based on our set of 12 predicted periods. In order to test the predictions for the RRab subset, which we might also refer to as the n = 10 → 9 and n = 9 → 8 systems, then we will have to rely upon smaller samples of very homogeneous systems observed in environments that maximize uniformity.
Fortunately the OGLE team has provided an excellent RR Lyrae star sample with which to test the hypothesized self-similarity in the RRab range of 0.45 days to 0.75 days.
Figure 3 shows the distribution of periods7 for 84 RR Lyrae variables found in the rich LMC star cluster NGC 1835.
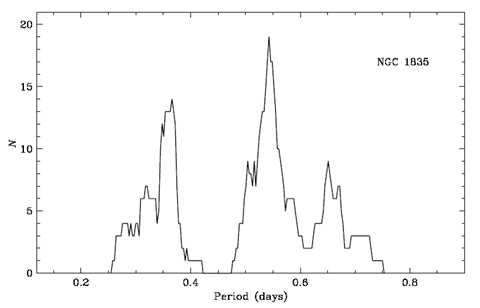
FIGURE 3 Histogram of periods for 84 RR Lyrae stars in the NGC 1835 cluster.7
To a first approximation we see the three familiar peaks at ≈ 0.3 days, ≈ 0.5 days and ≈ 0.7 days, but now significant substructure in the distribution has been revealed. The ≈ 0.3 days peak splits into a triplet structure with a dominant peak at 0.36 days, a smaller peak at 0.32 days and a still smaller peak at 0.28 days. The ≈ 0.5 days peak also has hints of a triplet structure with a dominant peak at 0.54 days, a clear shoulder at 0.50 days and another shoulder at 0.59 days. There is also a major peak centered at 0.66 days. Also notable are the major gap at 0.44 days and a minor gap centered at 0.62 days.
Table 4 demonstrates the correspondence between the observed features in the RR Lyrae period distribution for NGC 1835 and our set of predicted Stellar Scale analogues for the relevant 4He transition periods.
TABLE 4 OBSERVED AND PREDICTED PERIODS (NGC 1835)
Observed Feature (days) |
4He Transition |
Predicted Period (days) |
Error (days) |
0.28; peak |
1s8p – 1s7s (3S) |
0.2872 |
0.007 |
0.32; peak |
1s8p – 1s7s (1S) |
0.3223 |
0.002 |
0.36; peak |
1s8s – 1s7s (1S) |
0.3614 |
0.001 |
0.50; peak/sh. |
1s9s – 1s8s (3S) |
0.4997 |
0.0003 |
0.54; peak |
1s9s – 1s8s (1S) |
0.5317 |
0.008 |
0.59; shoulder |
1s10p – 1s9s (3S) |
0.5966 |
0.007 |
0.66; peak |
1s10p – 1s9s (1S) |
0.6615 |
0.002 |
0.71; peak |
1s10s – 1s9s (3S) |
0.7089 |
0.001 |
0.44; gap |
0.43 – 0.46 |
||
0.62; gap |
0.61 – 0.64 |
The results shown in Table 4 are fairly dramatic. We can match all of
the 8 peaks in the distribution to within ≤ 0.008 days. We can also understand
why the observed period distribution is a combination of discrete peaks;
why we tend to find primary peaks at ≈ 0.3
days (8→ 7 transitions), ≈ 0.5 days (9→ 8
transitions) and ≈ 0.7 days
(10→ 9 transitions); and why we can anticipate
gaps or valleys at 0.38 – 0.41 days, 0.43 – 0.46 days and 0.61 – 0.64
days. Depending on the eight physical factors discussed above, the
peaks and gaps can be shifted from their unperturbed positions. Also,
there is little doubt that randomness and differing transition probabilities
will result in variable amplitudes for the peaks. However, the results
achieved here suggest that unique, recognizable and quantifiable patterns
that can be best understood in terms of cosmological self-similarity will
be found in all RR Lyrae period distributions if sufficient effort is made
to keep the samples as homogeneous as possible in terms of masses, radii
and modes, and to analyze the period distributions with the statistical sophistication
employed by the OGLE team.
THE NEXT SET OF RESEARCH QUESTIONS
It is natural to ask whether there are readily identifiable analogues of 4He atoms undergoing transitions with 6 ≥ n ≥ 11, since the range for RR Lyrae stars (7 ≤ n ≤ 10) is only a small subset of possible transitions. The answer to this question is definitely in the affirmative. If we look at Table 2 we see that the shortest single-level 4He transitions yield predicted Stellar Scale analogue periods on the order of 0.0012 days. ZZ Ceti variables are white dwarf stars with typical masses of about 0.6 M¤, so they are primarily 4He analogues. Their range of periods2 is roughly 100 sec to 1000 sec, or 0.0012 days to 0.0116 days, which corresponds well with 1s2s → 1s1s and 1s3s → 1s2s transitions. W Virginis variables are also analogues of 4He, with masses2 of about 0.55 M¤. They are fundamental mode pulsators and their range of periods1,2 is roughly 1 to 71 days which corresponds to 11 ≤ n ≤ 43. Beyond that there are Mira variables with periods ranging from 90 days to at least 1374 days, which roughly corresponds to 46 ≤ n ≤ 500.
Given that there are more than 10 classes of variable stars, each with
their characteristic period, mode and mass ranges, there is obviously a huge
amount of work to be done before we can say that we have fully explored the
potential for physically meaningful analogies between variable stars and
atoms undergoing energy level transitions. For the present we can only
offer a preview of coming attractions in the form of the following table,
which lists some variable star classes and their probable Atomic Scale analogues.
TABLE 5 SOME VARIABLE STAR CLASSES AND ATOMIC ANALOGUES
Class of Variable Stars |
Mass Range (M¤) |
Period Range (days) |
Oscillat. Mode |
Likely Atomic Scale Analogue |
Probable n-Range |
Probable l |
ZZ Ceti |
≈ 0.6 |
0.001 – 0.012 |
Non-radial |
He |
3 ≥ n ≥ 1 |
l ≥ 1 |
d Scuti |
~ 2 |
0.05 – 0.2 |
Non-radial |
C, N, O? |
6 ≥ n ≥ 4 |
l ≥ 1 |
b Cepheid |
~11 - 15 |
0.13 – 0.29 |
Non-radial |
~ Se – Pd? |
8 ≥ n ≥ 5 |
l ≥ 1 |
RR Lyrae |
≈ 0.6 |
0.2 – 0.9 |
Radial |
He |
10 ≥ n ≥ 7 |
l = 0, 1 |
W Virginis |
≈ 0.6 |
1 - 71 |
Radial |
He |
43 ≥ n ≥ 11 |
l = 0, 1 |
Cepheid |
~ 3 - 16 |
1.4 - 71 |
Radial |
~ Ne - Cd |
43 ≥ n ≥ 12 |
l = 0, 1 |
Mira |
~ 1 |
90 - 1374 |
Radial |
He, Li |
500 ≥ n ≥ 46 |
l = 0, 1 |
CONCLUSION
Starting
from the SSCP’s self-similar scaling equations and our knowledge of
RR Lyrae stars, we were able to determine uniquely the mass of the
Atomic Scale analogues of RR Lyrae stars (helium), the relevant range
of principal quantum numbers (n = 7-10) and the relevant angular quantum
numbers (l =
0,1). Then we were able to verify that oscillations for the relevant
single-level transitions of 4He have periods that are well correlated
with RR Lyrae period distributions, as predicted by the Self-Similar
Cosmological Paradigm.
Introduction
One prediction mentioned in Paper #2 (see the “Selected Papers” section of this website) asserted that a specific Atomic Scale analogue to the Sun's 22-year magnetic activity cycle would eventually be discovered. The morphologies and motions of the structures involved in the magnetic field flipping should be similar for the analogues on both Scales, and their timescales should be related be the usual SSCP scaling equations. In this case,
Pstellar ≈ LPatomic ≈ (5.2 x 1017)(Patomic).
As discussed below, it appears that an excellent candidate for the Atomic Scale analogue to the Sun's 22-year magnetic reversal cycle, and related activity cycles in other stars, may have been identified.
The Solar Magnetic Reversal Cycle
The Sun's magnetic activity cycle is truly a remarkable physical process that is periodic and global, but enigmatic. The basic properties of the cycle have been observed and described with increasing sophistication since the time of Galileo, but a rigorous understanding of the physics that underlies the activity cycle has eluded scientists.
Starting at a time of minimum activity, which is characterized by low numbers of sunspots, new sunspots begin to form at mid-latitudes in both hemispheres. As the cycle proceeds the sunspot activity migrates toward the Sun's equator. The sunspots tend to come in pairs that have opposite polarities. During each half-cycle the leading spots in the pairs will tend to have one polarity in the Sun's northern hemisphere and the opposite polarity in the southern hemisphere. The polarities of the sunspot pairs reverse during the next half-cycle. The number of sunspots taking part in this migration from middle to low latitudes increases rapidly and remains at an elevated level until the Sun approaches a new activity minimum roughly 11 years later. At that time the Sun's global dipole magnetic field will have its “north” and “south” polarities reversed from what they were at the previous minimum. Two 11-year half-cycles are required for the system to return to its initial state, so the full cycle has a period of about 22 years.
When the solar activity cycle is studied over hundreds of years, it is found that half-cycle periods can vary in length from 8 years to 15 years with an average period of 11.1 years, that the amplitude of the sunspot numbers can vary by ≤ 3, that half-cycles can overlap by 2 to 3 years, that during the Maunder Minimum (1654 to 1715) there were very few sunspots at all, and that the establishment of the reversed magnetic fields at the North and South poles of the Sun can lag behind one another by up to 9 months. Despite the somewhat erratic nature of this phenomenon, which reminds one of a slightly cantankerous clock, the Sun's activity cycle has persisted for centuries with an average full-cycle period of 22.2 years.
An Atomic Scale Analogue?
The Sun's activity cycle is thought to take place primarily in a thick (≈ 0.3 R) outer layer of the Sun referred to as the convection zone. According to the SSCP, this outer spherical shell of charged matter in a plasma state corresponds to an S-state electron wavefunction representing the outermost electron of the inner core of a highly excited Rydberg atom. Such atoms, with their compact inner cores and nearly classical Rydberg electron orbiting very far from the core, are often called “planetary atoms” for obvious reasons.
We then ask whether electrons undergo processes associated with flipping of their intrinsic magnetic fields, and are led to the process of hyperfine electron spin transitions as the most promising category of potential analogues to what we are observing in the solar magnetic activity cycle. The simplest and best-known example of magnetic spin transitions on the Atomic Scale occurs in the ground state hydrogen atom. The proton and the electron of H both have spins of ½ and the total number of spin states is 2S + 1 = 2, representing spins parallel (both “up”) and spins anti-parallel (1 “up”, 1 “down”). In an environment that is cold enough to prevent excitation of the atom to n ³ 2 states, and where strong magnetic fields are absent, the H atom can undergo a transition from the higher energy parallel state to the lower energy anti-parallel state, emitting electromagnetic radiation with a frequency (n) of 1420 MHz. The period of this oscillation is 1/n = 0.704 x 10-9 sec. To convert this period into an analogous Stellar Scale period we multiply by the usual scaling factor of Λ (5.2 x 1017) for lengths and times: (0.704 x 10-9 sec)(5.2 x 1017) ¸ (3.17 x 107 sec/yr) = 11.62 years. It is encouraging that our initial test of the potential analogy gives results that are of the correct order of magnitude, and in fact are within a factor of 2.
As has been demonstrated elsewhere at this website, the mass of the Sun suggests that it is an analogue of Li rather than H. The unpaired outer electron of the ground state Li atom has a hyperfine spin transition with a frequency of about 803.5 MHz, which corresponds to an Atomic Scale period of 1.24 x 10-9 sec and an analogous Stellar Scale period of 20.5 years. That is rather close to 22.2 years! In the case of electron spin transitions involving spherical S-states, which would seem appropriate for the proposed analogy, electric dipole radiation is strictly forbidden and so the transition must proceed via magnetic dipole radiation. An oscillating magnetic dipole would seem to required in order to generate this type of electromagnetic radiation. Therefore we have identified potentially analogous processes on the Stellar and Atomic Scales that share some fairly unique qualitative properties and that appear to have periods that are reasonably well correlated by the SSCP's discrete self-similar transformation equations. Below we will explore this potential example of cosmological self-similarity in more detail.
Impediments To A More Quantitative Test Of The Analogy
If we wanted to do a more rigorous test of the proposed analogy between the solar magnetic cycle and a lithium atom undergoing a specific S-state hyperfine magnetic spin transition, we would have to know the internal configuration of the solar electron analogues. We know (Papers #1 and #2) that the outermost electron analogue for the solar system has a principal quantum number n of about 168, and an orbital quantum number l that is nearly equal to n. Given the radius of the Sun's convection envelope and the 160 minute oscillations of the Sun's surface layers, it has been previously concluded that the outer electron analogue of the system's core has n = 5 and is in an S-state with l = 0. The problem is that a neutral lithium atom analogue would have one more electron analogue well inside the core, below the convective layer. Its n value could be any number between 1 and 4. Even more problematic is the fact that the Sun could also be analogous to the core of a Li+ ion with no interior electron analogue, or it could be analogous to a Li- ion with 2 internal electron analogues in unknown states. (Note: As if all these uncertainties were not enough, there is also the possibility that the correct spin transition analogy involves electron spin resonance wherein external magnetic fields and electromagnetic radiation drive the system at a specific oscillation frequency.)
It is conceivable that with a lot of astute physics, and working on both the atomic and stellar ends of the puzzle, one might be able to use a chain of reasoning to narrow down the set of possible electron configurations that apply in the proposed analogy. Detailed studies of this type will have to remain a project for the future. What can be done at present is to take a broader look at magnetic activity cycles in other stars to see if they exist and, if so, how their cycle periods compare with the distribution of periods for hyperfine transitions in atoms.
Magnetic Activity Cycles In Other Stars
If our analogy to hyperfine spin transitions is valid, then we would expect that some other stars have activity cycles similar to the Sun's and others do not. Atoms must have the right configuration in order for hyperfine transitions to occur. In atoms with filled electron shells and no unpaired electrons, the hyperfine transitions cannot occur. The ground state of helium is one example and a Li+ ion with both electrons in the same S-shell is another. Since hyperfine spin transitions are fairly common, our analogy would be considerably weakened if other stars did not have magnetic activity cycles. On the other hand, if all stars had them, then the analogy would also be weakened.
Fortunately for the proposed analogy the observations verify the expected dichotomy: some stars have activity cycles and some apparently do not. The most extensive study of magnetic activity cycles in stars has been carried out at the Mt. Wilson Observatory. Since the program began in 1966, over 100 stars of spectral types F, G, K and M have been monitored for indications of cyclical magnetic activity. In 1995 the results for 112 stars, including the Sun, were reported (Baliunas, et al, 1995). Thirty-one stars were observed to have flat or linear baselines, suggesting no cyclic activity or extremely long timescales. Twenty-nine stars had irregular variations in their magnetic activities but lacked periodic cycles. Fifty-two stars were observed to manifest periodic magnetic activity cycles with estimated half-cycle periods ranging from 2.5 years to 25 years. The quality of the observational estimates for the cycle periods were rated either excellent, good, fair or poor. Below is a table of the magnetic cycling stars in the good and excellent categories.
| Star | Spectral Type |
Observed Magnetic |
Presumed* Full Cycle |
Quality of Cycle |
|
Sun |
G2 V |
10.0 ± 0.1** |
20.0** |
Excellent |
|
HD 3651 |
K0 V |
13.8 ± 0.4 |
27.6 |
Good |
|
HD 4628 |
K4 V |
8.37 ± 0.08 |
16.8 |
Excellent |
|
HD 10476 |
K1 V |
9.6 ± 0.1 |
19.2 |
Excellent |
|
HD 16160 |
K3 V |
13.2 ± 0.2 |
26.4 |
Excellent |
|
HD 26965 |
K1 V |
10.1 ± 0.1 |
20.2 |
Excellent |
|
HD 32147 |
K5 V |
11.1 ± 0.2 |
22.2 |
Excellent |
|
HD 78366 |
G0 V |
12.2 ± 0.4 |
24.4 |
Good |
|
HD 81809 |
G2 V |
8.17 ± 0.08 |
16.4 |
Excellent |
|
HD 103095 |
G8 VI |
7.30 ± 0.08 |
14.6 |
Excellent |
|
HD 114710 |
G0 V |
16.6 ± 0.6 |
33.2 |
Good |
|
HD 115404 |
K1 V |
12.4 ± 0.4 |
24.8 |
Good |
|
HD 149661 |
K0 V |
17.4 ± 0.7 |
34.8 |
Good |
|
HD 152391 |
G7 V |
10.9 ± 0.2 |
21.8 |
Excellent |
|
HD 156026 |
K5 V |
21.0 ± 0.9 |
42.0 |
Good |
|
HD 160346 |
K3 V |
7.00 ± 0.08 |
14.0 |
Excellent |
|
HD 166620 |
|
15.8 ± 0.3 |
31.6 |
Excellent |
|
HD 201091 |
K5 V |
7.3 ± 0.1 |
14.6 |
Excellent |
|
HD 201092 |
K7 V |
11.7 ± 0.4 |
23.4 |
Good |
|
HD 219834A |
G5 IV-V |
21 ± 1 |
42 |
Good |
|
HD 219834B |
|
10.0 ± 0.2 |
20.0 |
Excellent |
* Here we presume that the observed cycle is a half-cycle, as is known to be the case for the Sun.
** Longer term averages that take all aspects of the cycle into account are 11.1 years for the half-cycle and 22.2 years for the full cycle.
From the stellar data presented in the table above we can see that the periods of the presumed full cycles range from 14 years to 42 years, with an average of about 24.3 years. Shorter periods are favored in the analysis so the apparent cutoff at about 14 years, or more conservatively on the order of 10 years, can be considered potentially important and diagnostic. The available data strongly select against long-period cycles, so they are probably under-represented. In the case of very long periods, say 100 years or more, no star other than the Sun has been studied for a sufficiently long time to properly define these periods. The Sun is believed to have long-term amplitude variations in its cycle with periods of about 80-90 years (the Gleissberg cycle) and about 150-210 years (the Suess cycle) (Bonev, et al, 2004).
Hyperfine Spin Transitions
For comparison we will look at some typical Atomic Scale hyperfine spin transition periods for low-mass atoms in states with low n and l values, since the relevant stars in the comparison are relatively small, low-mass systems. The table below also shows predicted periods for Stellar Scale analogues to the specific transition periods.
|
Atom (configuration) |
Frequency (MHz) |
Period (sec) |
Predicted Stellar Scale |
|
H (1s 2S1/2) |
1420.4 |
7.04 x 10-10 |
11.62 |
|
Li (1s22s 2S1/2) |
803.5 |
1.24 x 10-9 |
20.54 |
|
Li (1s23s 2S1/2) |
189.4 |
5.20 x 10-9 |
87.16 |
|
H (2s 2S1/2) |
177.6 |
5.63 x 10-9 |
92.95 |
|
Li- (1s2p3 5S) |
95.4 |
1.04 x 10-8 |
173.04 |
|
Li (1s22p 2P1/2) |
92.0 |
1.08 x 10-8 |
179.43 |
|
H (2p 2P1/2) |
59.2 |
1.69 x 10-8 |
278.85 |
|
H (3s 2S1/2) |
52.6 |
1.90 x 10-8 |
313.84 |
|
H (4s 2S1/2) |
22.2 |
4.50 x 10-8 |
743.60 |
|
H (4p 2P1/2) |
7.4 |
1.35 x 10-7 |
2230.80 |
|
H (3p 2P3/2) |
7.0 |
1.43 x 10-7 |
2358.27 |
|
H (4d 2D3/2) |
1.8 |
5.55 x 10-7 |
9171.08 |
When we compare the scaled electron spin transition periods with the presumed full cycle periods of the stars, we see that the agreement is reasonably good at the short-period end of the ranges but not at the long-period end. As mentioned above, in addition to its primary 22.2-year cycle period the Sun has secondary cycling oscillations at about 80-90 years and about 150-210 years. In the case of other stars, however, astronomers currently do not have the capability to test for magnetic activity cycles with periods on the order of 102 years to 104 years.
A serious concern is that the number of stars in the Sun's neighborhood that are undergoing magnetic activity cycles appears to be on the order of 50%. Given that hyperfine transitions tend to have low (and sometimes very low) probabilities, 50% is a very high number. This might suggest that these magnetic activity cycles are driven by resonant forcing in analogy to the phenomenon of electron spin resonance, rather than our original analogy to spontaneous spin transitions.
A Very Speculative Possible Solution
From the discussion above, we have seen that the Sun's magnetic activity cycle appears to have four relevant periods: 11.1 years, 22.2 years, 80-90 years and 150-210 years. Consider the following table of data.
|
Solar Cycle Periods (years) |
Orbital Periods Of Outer Planets (years) |
|
11.1 |
11.9 (Jupiter) |
|
22.2 |
29.5 (Saturn) |
|
80-90 |
84 (Uranus) |
|
150-210 |
165 ( |
Is it coincidental that the orbital periods of the Solar System's four major planets closely parallel the four main periods of the solar cycle? Perhaps not. Within the conceptual framework of the SSCP, the planetary system constitutes an analogue to the wavefunction for one electron in a very high-n Rydberg state (n ≈ 168 and l ≈ n). It is conceivable that for a lithium atom with the unusual configuration described in this study, the Rydberg electron can resonantly drive the spin transition of the n = 5, l = 0 outer core electron to resonate at the orbital frequencies of the Rydberg electron's wavefunction. By analogy, the Sun's magnetic activity cycle might not be self-similar to a spontaneous spin transition, but rather to resonant spin transitions regulated by interactions with the planetary system. This is an admittedly wild idea, but an interesting one no less. If other stars with well-documented activity cycles were found to have planetary systems with similar correspondences between orbital and cycle periods, then this wild idea might be worthy of very serious consideration. A preliminary but hopeful sign is that the stars HD 179949 and n And have chromospheric activity cycles that appear to be coupled to the orbital periods of close-in Jupiter-mass planets (Shkolnik et al, 2005). These authors note that since the enhanced activity occurs once per orbit, the interaction is probably electromagnetic in origin, rather than tidal.
Final Thoughts
The present work on the potential self-similarity between electron spin transitions and magnetic activity cycles in stars can only be viewed as a rudimentary beginning. It remains to be seen whether more thorough and sophisticated research will support the proposed self-similarities, or falsify them.
The SSCP predicts that ultracompact objects with extremely high densities comprise the overwhelming majority of the mass/energy found on each of the three observable cosmological Scales (Atomic, Stellar and Galactic). Atomic nuclei play this dominant role on the Atomic Scale, while the analogous class of self-similar nuclear objects on the Stellar Scale includes neutron stars (observed) and predicted stellar-mass black holes (possibly detected in dark matter microlensing experiments). Based on their sizes, shapes and central singularities, the SSCP identifies galaxies as the Galactic Scale counterparts to Atomic Scale particles and nuclei under high energy and density conditions.
Rotation and Oscillation Periods for Atomic, Stellar and Galactic Scale "Nuclei" |
||
| Typical Rotation Period | Typical Oscillation Period | |
| Atomic Nuclei | 5 x 10-20 sec |
1 x 10-21 sec |
| Neutron Stars | 3 x 10-2 sec |
5 x 10-4 sec |
| Active Galaxies | 1 x 1016 sec (3 x 108 yr) | 2.5 x 1014 sec (8 x 106 yr) |
Two reasonably fundamental physical properties of these ultracompact objects on the three different Scales are their typical rotational and oscillatory periods, since these periods are closely related to the spin and mass/energy of the objects, respectively. If the SSCP is a useful paradigm and the correct self-similar analogues have been chosen, then the rotation and oscillation periods for these analogues should obey the basic self-similar scaling relation that governs temporal phenomena:
PN ≈ LPN-1 ,
The Table above shows that our expectations for the relationships among the rotational and oscillatory periods for the proposed Atomic, Stellar and Galactic Scale analogues are met. At the time that these relationships were initially tested (papers #1 and #2), the typical oscillation period of ≈ 107 years for active galaxies could only be predicted, since galactic oscillations had not been observed yet. In the last 10 years this situation has changed and it appears that another SSCP prediction may have been vindicated.
Bearing in mind that only a subset of galaxies would be undergoing global oscillations at any given epoch, it appears that there is now a growing body of evidence supporting the idea that massive active galaxies can eject energy and matter in periodic pulsations with timescales typically on the order of 107 years, as predicted by the SSCP.
Smallest Red Dwarfs
Papers #1 and #2 in the “Papers” section show how to calculate the Stellar Scale equivalent of the Bohr radius (a0 = 0.53 x 10-8 cm), which is identified as A0 and is ≈ (a0)(Λ) ≈ (0.53 x 10-8 cm)(5.2 x 1017) ≈ 2.76 x 109 cm.
In the Atomic Scale case, the electron’s wave function for the hydrogen atom peaks at a0, but extends beyond that radius to approximately 3a0. A simple test of the SSCP is whether or not low-mass (M ≤ 0.2 M¤) red dwarf stars have a minimum radius of about 8.3 x 109 cm ( ≈ 3A0). When papers #1 and #2 were written in 1988, the minimum radius for a red dwarf star was estimated to be about 8.7 x 109 cm, which was in reasonably good agreement with the predicted value. In 2005 a European team analyzing transiting star data from the Optical Gravitational Lensing Experiment reported a new observational estimate for the smallest red dwarf radius of 8.35 x 109 cm (Pont, F., et al, Astron.& Astrophys. 433, L21-L24, 2005), which is quite close to the predicted value. This measurement is a “direct radius determination” that involves fewer assumptions and uncertainties than previous methods.
The wave function cutoff at 3a0 is a fairly crude approximation, but the peak at a0 is a better-defined physical parameter. At some point in the future it may be possible to infer the inner mass distribution of the lowest-mass red dwarf stars. The SSCP uniquely predicts a distinct and dominant peak in the mass distribution of the star’s outer layers at A0 ( ≈ 2.8 x 109 cm) for these smallest red dwarf stars.
Largest Star
Atoms in very high Rydberg states can be relatively gigantic, literally comparable to the size of a small microbe. In 1988 (paper #1) the largest atoms commonly observed had a principle quantum number of ≈ 110, which translates into a radius of 12,100 a0 or nearly 0.001 millimeters! At that time the largest observed stars had radii on the order of 12,140 A0 or about 3.4 x 1013 cm. In 2004 the star VY CMa set a new radius record at a humongous 3020 R¤, or about 2.1 x 1014 cm, which is approximately 76,594 A0 (Monnier, J.D., et al, Astrophys. J. 605, 436, 2004). According to the SSCP this would correspond to a Rydberg atom with a principal quantum number of at least 195 if the outer radius is about 2 times the radius of the mass density peak, and could be as high as 276 in the case of a very thin outer envelope. Although the critical distance and luminosity estimates for VY CMa are “fairly certain” and “well-established”, respectively, it has been noted that “none of [VY CMa’s] stellar properties are in accord with stellar evolution theory” (Levesque, E.M., et al, Astrophys. J., in press, 2005, [arXiv:astro-ph/054337]). The SSCP predicts that the observed sizes of the largest atoms and the largest stars will continue to be of the same order of magnitude when scaled by the Rstar ≈ ΛRatom relation.
Stellar Mass Limits
A much more important, and potentially more rigorous, test of the Self-Similar Cosmological Paradigm concerns mass limits for stars. At the start of the 21st century the most widely accepted theories for the formation and evolution of stars put no well-defined upper limit on the mass of a star. Supermassive stars of over 300 M¤ were considered to be possible. Conversely, the SSCP predicted that single stars, like atoms, have an upper mass limit due to strict stability constraints. For the Atomic Scale, the most massive naturally occurring atoms have masses of about 240 times the mass of the proton. Since we have already determined that the Stellar Scale equivalent of the proton mass is ≈ 0.145 M¤, we can predict that the largest masses for single stars will be on the order of (240)(0.145 M¤), or roughly 35 M¤. Observationally we find that stars with masses greater than 20 M¤ are quite rare, less than one per thousand stars (Reid, I.N., et al, Astron. J. 124, 2721-2738, 2002). Very recently it was reported (Figer, D.F., Nature 434, 192-194, 2005) that for the Arches cluster, an environment favoring the formation of very massive stars, the most massive stars were estimated to have masses of about 130 M¤. This figure is about 3.7 times larger than the SSCP prediction, but the values are of the same order of magnitude, and one must bear in mind that mass estimates for stars at the upper and lower ends of the stellar mass scale are based on numerous theoretical assumptions, making significant systematic errors a definite possibility. The main message is that astrophysicists now suspect that stars, like atoms, appear to have an upper mass limit. A mass cutoff below 150 M¤ has no clear explanation within previous stellar formation/evolution theories, but was predicted by the SSCP. We may further predict that the observed upper mass limit will gradually decrease and eventually agree with the SSCP prediction for the scaled upper mass limit for atoms.