At first glance, this seems like a joke (a physicist's joke), but one which might (in theory) save you a tiny bit of postage money. After all, if some of the bees aren't even touching the inside of the box, how can they affect the reading on the scale? But then think about what really happens when you, say, stand on a scale with your shoes on. Surely the scale reading will correspond to a lot more than just your shoes (or the soles of your shoes).
Well, it is just a joke, and it won't work, not even in theory, but it takes a bit of thought and care to prove that it won't work.
Let's see why it won't work. You might start out by thinking about the forces that the surface of the scale and the bottom of the box exert on each other, the gravitational forces exerted by the earth on the bees and on the various parts of the box, the force that a flying bee exerts on the air under it, the forces that the air in the box exerts on the insides of the box, even the forces that one part of the box exerts on other parts (to hold the box together), etc., etc., etc. If you follow that route, you will quickly drown in a morass of diagrams and equations.
(We are about to invoke a "theorem" that is familiar to almost every physics student. The theorem also is pretty reasonable: all it says is that if a collection of objects - in this case, bees and box - is at rest, the total force on it is zero. But if you are suspicious of this theorem, as something pulled out of the hat by a physics professor, then you may want to get into that "morass" that we just warned about -- Go down to the end of this discussion for a brief discussion from this point of view.)
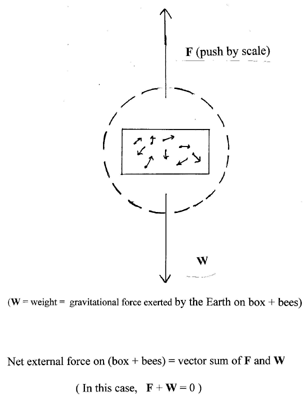
We suppose that there are quite a few bees in the box and that at any given moment some are resting, and the flying ones are all flying in various directions - some up, some down, some sideways - and about the same number going up at any given moment as are flying down. So, even though there is motion within the box, when the box is on the scale, the center of mass of box & bees is at rest and certainly has an acceleration (as well as velocity) equal to zero. Therefore we know that the total external force on that composite system is zero.
That's a special case of a general and very powerful theorem: The total external force on any collection of objects (a "system" in physics jargon) is equal to the total mass of that system times the acceleration of the center of mass of the system. That theorem can be derived by applying Newton's first and second laws to all the parts of that system.That total external force is the sum (the vector sum) of the gravitational force downward (the "weight" of that system - box & bees) and the upward push of the scale. The latter force is what the scale measures, and that is the force that determines how much postage you will have to pay. If the total force is zero, then the upward push of the scale must equal in size the weight of box & bees, no matter whether the bees are resting on the inside of the box or buzzing about. So the idea won't work.
Often we emphasize the application of that theorem by drawing what is called a "free body diagram" of the system. Draw a mental box around the system, and draw vectors representing all the external forces on the parts of that system. (Only the external forces; in this case we must not include things like forces that the sides of the box may be exerting on the bees.) Such a diagram is really just a convenient way of making a list of the external forces. Here is one for the present situation:

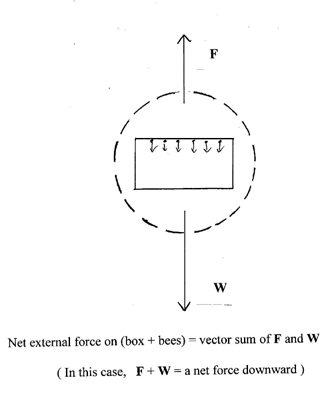
Here are a few ways in which (in principle, not in practice!) these conclusions might be modified. If you could train the bees (!) to hang onto the upper side of the interior of the box and then let go in unison and go into free fall just as the box is placed on the scale, then the center of mass of the whole system would for a fraction of a second be accelerating downward. Therefore the net external force would be non-zero, and in the downward direction. Since the gravitational force on bees & box is unchanged, even though the bees are falling, the only way we could have a net downward force is for the upward force exerted by the scale to be a little bit less - saving a little postage, if it works. Here's a free body diagram for that situation:
Or if the box, instead of being closed, were an open wire cage, then maybe air currents could enter or leave through the top and sides in funny ways, and then our simple conclusions might be off (a little bit).
Now, here is another consideration, of effects that are really, really small! What if the bees were buzzing around very fast, at speeds that are getting up toward the speed of light? One of the results of Einstein's special theory of relativity is that they act as if their mass were a little bit larger. That would make their masses a tiny bit heavier and (in principle) it seems as if this might have the effect of costing you extra postage. However, the bees would have to burn "fuel" (consume a bit of their body mass) to get up to speed, and that would cancel out that apparent increase in mass that they would have because of their speed. And besides, this would all have the effect of heating up the air and that extra energy could get lost to the outside, and (Einstein again) that loss of energy would show up as an equivalent loss of mass of the whole box & bees system, so you could save some postage money after all. Let me emphasize that - because of the numbers involved - all of the discussion in this paragraph is truly silly; these effects are absolutely negligible even for hypothetical supersonic bees. (Even a bee flying at the speed of sound is only going at about one millionth of the speed of light.)
We analyzed this problem with the aid of a simple and powerful
theorem. Good old Newton's Second Law, F = ma, applies to a collection
of objects (a "system") if m means the total mass, F the total external
force, and a the acceleration of the center of mass of the system. If
we know the acceleration of the center of mass (zero in the case of normal,
untrained bees), then we know the total external force, and if we already know
one of the external forces (the gravitational force), then we can easily figure
out the other one (the push of the scale). That's much simpler than trying to
think about how much a resting bee, say, pushes downward on the inside of the
box, how hard the box pushes back, etc., etc. As we said at the beginning, it's
easy to lose track of a force or two or get a sign wrong, and one could easily
convince one's self that the silly idea has merit. But the elegant theorem we
used provides a very simple answer to what might otherwise be a complicated
problem and tells us there is no need to bother getting bogged down in the details
of what forces are being exerted inside the box.
(By the way, we have been talking about the system consisting
of the box and the bees. We really should have included also the air in the
box, but that wouldn't have affected our conclusion, since in the case of the
box on the scale, with the bees buzzing in all directions, the center of mass
of the air would not be accelerating, even though there might be some transient
air currents. If we were serious about the "trained bees" scenario,
then we probably should go back and think about the air more carefully in that
case.)
What if you don't want to accept the "theorem" that we invoked near the beginning of this discussion. Well, suppose first that all your bees are asleep inside, on the floor of the box. In that case, it certainly seems reasonable to suppose that the weight registered by the scale is that of box and bees together. And now suppose they are buzzing around inside. Consider just one of the bees, for simplicity. He (or she) is not in contact with the material of the box at all. So how does the scale "know" the bee is there? The air must be pushing up on the underside of the bee. So the bee's wings are pushing down on the air. Since the air isn't going anywhere, the material of the bottom of the box must be pushing up, more than it was before, on the air, the air is pushing down on the bottom of the box, and so on. The result must be that the scale is pushing up harder on the box than it would be if the box were empty. So the postage-avoidance scheme doesn't work. End of story, from this second point of view. It's really just like you and your shoes on a scale. Your shoes alone might weigh, say, 2 pounds. But when you're in them, you are pushing down on the shoes with a force of, say, 150 pounds. The earth's gravity is exerting a downward force on the shoes of 2 pounds. Since the shoes aren't moving, the scale must be pushing upward with a force that balances those two forces, i.e., 152 pounds.